코딩테스트/알고리즘 (Python) ★★★
[자료구조5] 트리
개발자딥게
2022. 7. 26. 11:49
반응형
트리 구조
트리 (Tree) 구조
- 트리: Node와 Branch를 이용해서, 사이클을 이루지 않도록 구성한 데이터 구조
- 실제로 어디에 많이 사용되나?
- 트리 중 이진 트리 (Binary Tree) 형태의 구조로, 탐색(검색) 알고리즘 구현을 위해 많이 사용됨
알아둘 용어
- Node: 트리에서 데이터를 저장하는 기본 요소 (데이터와 다른 연결된 노드에 대한 Branch 정보 포함)
- Root Node: 트리 맨 위에 있는 노드
- Level: 최상위 노드를 Level 0으로 하였을 때, 하위 Branch로 연결된 노드의 깊이를 나타냄
- Parent Node: 어떤 노드의 다음 레벨에 연결된 노드
- Child Node: 어떤 노드의 상위 레벨에 연결된 노드
- Leaf Node (Terminal Node): Child Node가 하나도 없는 노드
- Sibling (Brother Node): 동일한 Parent Node를 가진 노드
- Depth: 트리에서 Node가 가질 수 있는 최대 Level
이진 트리(Binary Tree)와 이진 탐색 트리 (Binary Search Tree)의 차이점
- 이진 트리: 노드의 최대 Branch가 2인 트리
- 이진 탐색 트리 (Binary Search Tree, BST): 이진 트리에 다음과 같은 추가적인 조건이 있는 트리
- 왼쪽 노드는 해당 노드보다 작은 값, 오른쪽 노드는 해당 노드보다 큰 값을 가지고 있음!
자료 구조 이진 탐색 트리의 장점과 주요 용도
- 주요 용도: 데이터 검색(탐색)
- 장점: 탐색 속도를 개선할 수 있음
- 단점: 복잡
이진 탐색 트리의 시간 복잡도와 단점
1. 시간 복잡도 (탐색시)
- depth (트리의 높이) 를 h라고 표기한다면, O(h)
- n개의 노드를 가진다면, ℎ=𝑙𝑜𝑔2𝑛h=log2n 에 가까우므로, 시간 복잡도는 𝑂(𝑙𝑜𝑔𝑛)O(logn)
- 참고: 빅오 표기법에서 𝑙𝑜𝑔𝑛logn 에서의 log의 밑은 10이 아니라, 2입니다.
- 한번 실행시마다, 50%의 실행할 수도 있는 명령을 제거한다는 의미. 즉 50%의 실행시간을 단축시킬 수 있다는 것을 의미함
- 참고: 빅오 표기법에서 𝑙𝑜𝑔𝑛logn 에서의 log의 밑은 10이 아니라, 2입니다.
2. 이진 탐색 트리 단점
- 평균 시간 복잡도는 𝑂(𝑙𝑜𝑔𝑛)O(logn) 이지만,
- 이는 트리가 균형잡혀 있을 때의 평균 시간복잡도이며,
- 다음 예와 같이 구성되어 있을 경우, 최악의 경우는 링크드 리스트등과 동일한 성능을 보여줌 ( 𝑂(𝑛)O(n) )
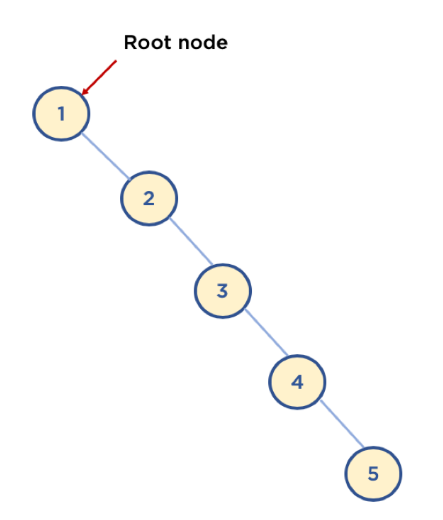
파이썬으로 이진탐색트리 구현하기
1. 노드 클래스 만들기
class Node:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
2. 이진 탐색 트리에 데이터 넣기
class NodeManagement:
def __init__(self, head):
self.head = head
def insert(self, value):
self.current_node = self.head
while True:
# 왼쪽 방향
if value < self.current_node.value:
# 왼쪽에 노드 있다면 계속 순회
if self.current_node.left != None:
self.current_node = self.current_node.left
# 왼쪽에 노드 없다면 노드 생성 후 연결
else:
self.current_node.left = Node(value)
break
# 오른쪽 방향
else:
self.current_node = self.current_node.right
if self.current_node.right != None:
self.current_node = self.current_node.right
else:
self.current_node.right = Node(value)
break
head = Node(1)
BST = NodeManagement(head)
BST.insert(2)
3. 이진탐색트리에 특정데이터 있는지 탐색하기
def search(self, value):
self.current_node = self.head
while self.current_node:
# 찾았으면 True 반환
if self.current_node.value == value:
return True
# 왼쪽 방향
elif self.current_node.value > value:
self.current_node = self.current_node.left
# 오른쪽 방향
else:
self.current_node = self.current_node.right
# 데이터가 없음
return False
BST.search(1) # True
BST.search(100) # False
4. 이진탐색트리 노드 삭제하기
case 1. leaf node 삭제하기
case 2. child node 가 1개 있는 노드 삭제하기 좌O, 우X
case 3. child node 가 1개 있는 노드 삭제하기 좌X, 우 O
case 4. chile node 가 2개 있는 노드 삭제하기
def delete(self, value):
searched = False
self.current_node = self.head
self.parent = self.head
while self.current_node:
# 삭제할 노드 찾음
if self.current_node.value == value:
searched = True
break
elif self.current_node > value:
self.parent = self.current_node
self.current_node = self.current_node.left
else:
self.parent = self.current_node
self.current_node = self.current_node.right
# current_node: 삭제할 노드 / parent: 그 부모 노드
if searched == True:
# ----- case1. leaf node -----
if self.current_node.left == None and self.current_node.right == None
if self.parent.value > value: # 좌 노드
self.parent.left = None
else: # 우 노드
self.parent.right = None
del self.current_node
# ----- case2. one left child node -----
elif self.current_node.left != None && self.current_node.right == None:
if self.parent.value > value:
self.parent.left = self.current_node.left
else:
self.parent.right = self.current_node.left
del self.current
# ----- case3. one right child node -----
elif self.current_node.left == None && self.current_node.right != None:
if self.parent.value > value:
self.parent.left = self.current_node.right
else:
self.parent.right = self.current_node.right
del self.current
# ----- case4. two child node -----
elif self.current_node.left != None and self.current_node.right != None
# 삭제노드가 부모노드의 왼쪽에 있을때
if self.parent.value > value:
# 오른쪽에서
self.change_node = self.current_node.right
self.change_node_parent = self.current_node.right
# 가장 작은 값을 찾음
while self.change_node.left:
self.change_node_parent = self.change_node
self.change_node = self.change_node.left
# 가장 작은 노드가 오른쪽 child 있다면
if self.change_node.right != None:
self.change_node_parent.left = self.change_node.right
# child 없다면
else:
self.change_node_parent.left = None
#current노드를 chaneg노드로 바꾸기
self.parent_node.left = self.change_node
self.change_node.left = self.current_node.left
self.change_node.right = self.current_node.right
# 삭제할 노드의 메모리 해제
del self.current_node
# 삭제노드가 오른쪽에 있을때
elif self.parent.value < value:
# 오른쪽에서 가장
self.change_node = self.current_node.right
self.change_node_parent = self.current_node.right
# 가장 작은 값을 찾음
while self.change_node.left:
self.change_node_parent = self.change_node
self.change_node = self.change_node.left
# 가장 작은 노드가 오른쪽 child 있다면
if self.change_node.right != None:
self.change_node_parent.left = self.change_node.right
# child 없다면
else:
self.change_node_parent.left = None
#current노드를 change노드로 바꾸기
self.parent_node.right = self.change_node
self.change_node.left = self.current_node.left
self.change_node.right = self.current_node.right
# 삭제할 노드의 메모리 해제
del self.current_node
return True
# 삭제할 노드가 이진탐색트리 내에 없음
else:
return False
5. 코드 테스트
- random 라이브러리 활용
- random.randint(첫번째 숫자, 마지막 숫자): 첫번째 숫자부터 마지막 숫자 사이에 있는 숫자를 랜덤하게 선택해서 리턴
예: random.randint(0, 99): 0에서 99까지 숫자중 특정 숫자를 랜덤하게 선택해서 리턴해줌
import random
# 0~999사이 랜덤값 100개 저장(중복없음)
bst_nums = set()
while len(bst_nums) != 100:
bst_nums.add(random.randint(0,999))
# 이진탐색트리 구조 생성 후 값 입력
head = Node(500)
BST = NodeManagement(head)
for i in bst_nums:
BST.insert(i)
# 100개 노드 전체를 이진탐색 시작
for idx, num in enumerate(bst_nums):
if BST.search(num) == False:
print("search fail")
# 삭제하고자 하는 값 10개 저장(중복없음)
delete_num = set()
bst_nums = list((bst_nums)) # set -> list 형변환
while len(delete_num) != 10:
delete_num.add(bst_nums[random.randint(0,99)])
for i in delete_num:
if BST.delete(i)==True:
print("삭제 성공")
elif BST.delete(i)==False:
print("삭제 실패")
반응형